삽입 정렬(Insertion Sort), 병합 정렬(Merge Sort)

정렬이 필요한 이유?

많은 문제들이 일단 정렬이 된 이후엔 훨씬 해결하기 쉬워짐

• 중간값을 찾는 문제
• 이진 탐색
• 데이터 압축
• 컴퓨터 그래픽 등

삽입 정렬(Insertion Sort)

• 이미 정렬된 A[0:i-1] 배열에 A[i] 를 비교해가며 올바른 위치에 삽입될 때까지 자리를 바꾼다.

• 모든 배열 요소에 대해서(θ(n)), θ(n) 만큼의 비교와 swap이 필요 => θ(n^2)

  > 비교와 swap의 작업량의 크기는 거의 비슷하다고 가정

이진 삽입 정렬(Binary Insertion Sort)

• A[0:i-1] 은 이미 정렬되어 있기 때문에 삽입할 자리를 찾을 때 Binary search를 이용한다.
• Binary search 자체는 θ(logn) 이지만 삽입 이후 나머지 element들을 shift하는데 θ(n) 의 작업량을 가지므로 결과적으로 똑같이 θ(n^2)

병합 정렬(Feat. Divide and Conquer)

배열 A를 L 과 R 로 분할하고 각각을 정렬한 L' 과 R' 을 병합하는 방법

1. n = 1 이면 완료.
2. 그 외의 경우엔 재귀적으로 A[1, ..., n / 2] 와 A[n / 2 + 1, ..., n] 을 정렬한다.
3. 정렬된 두 sub-array들을 병합한다.

Merge 방식

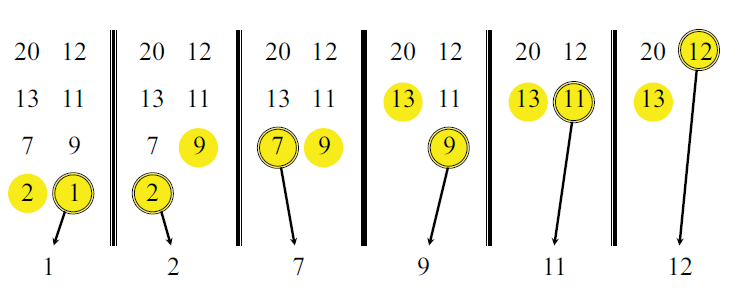
좌우를 비교하며 작은 값을 가져와서 배열에 채워준다.

병합정렬의 복잡도 분석

θ(cn * (1 + lgn)) = θ(nlogn)

공간 복잡도

• 삽입정렬의 경우 in-place 로 정렬되므로 공간 복잡도는 θ(1)
• 병합 정렬의 경우 θ(n)